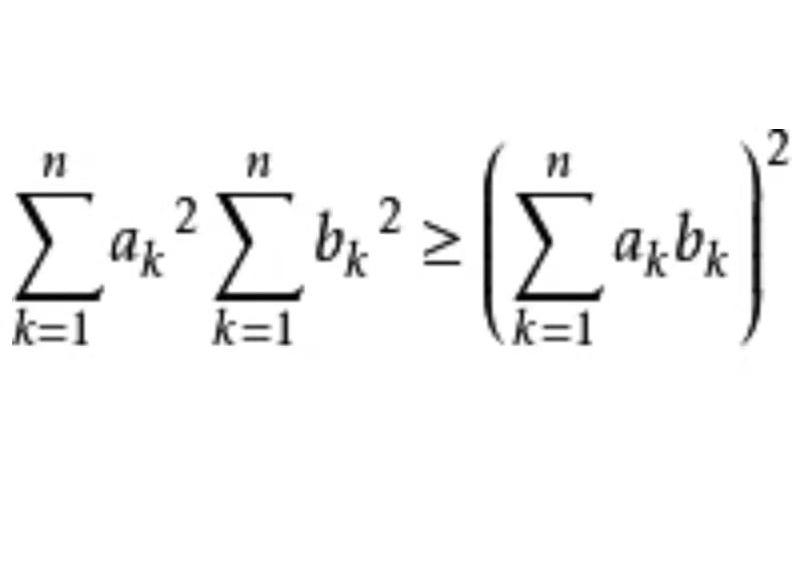定義
指形如akbk2≤a2kb2k的不等式,其中ak,bk(k=1,2,…,n)為實數,等号當且僅當ak,bk(k=1,2,…,n)成比例,即時成立.它是最常用的不等式之一,由柯西(Cauchy,A.-L.)于1821年發表。
推導過程
柯西不等式柯西不等式擁有多種形式,下面是其幾種形式。
二維形式:(a2+b2)(c2+d2)≥(ac+bd)2,等号成立條件:ad=bc
三角形式:,等号成立條件:ad=bc
向量形式:|α||β|≥|α·β|,α=(a1,a2,…,an),β=(b1,b2,…,bn)(n∈N,n≥2),等号成立條件:β為零向量,或α=βλ(λ∈R).
一般形式:等号成立條件:a1:b1=a2:b2=an:bn或ai、bi均為零.
推廣形式:(x1-y1-…)(x2-y2-…)…(xn-yn-…)
直接法
設
則
所以,即
利用二次型
即關于x,y的二次型非負定,那麼
即
數學歸納法
當n=1時,a12b12≥(a1b1)2不等式顯然成立
設
當n=k+1時
而
即n=k+1時,不等式成立
定理推廣
若函數f(z)在區域D及其邊界上解析,a為D内一點,以a為圓心做圓周CR:|z-a|=R,隻要CR及其内部G均被D包含,則有:
其中M是|f(z)|的最大值。
所以:
應用
柯西不等式在求某些函數最值中和證明某些不等式時是經常使用的理論根據,我們在教學中應給予極大的重視。正柯西不等式是高中數學中新引人的一個重要不等式,它的出現使得函數的最值問題又多了一條解決途徑。
巧拆常數證不等式
例:設a、b、c為正數且互不相等。求證:2/(a+b)+2/(b+c)+2/(c+a)>9/(a+b+c)
證明:如果了解柯西不等式,那麼很簡單
(a+b+b+c+c+a)*[1/(a+b)+1/(b+c)+1/(c+a)]>9
=>2/(a+b)+2/(b+c)+2/(c+a)>9/(a+b+c).
附證:設2x=a+b,2y=b+c,2z=c+a,則所證不等式等價于
1/x+1/y+1/z>9/(x+y+z)
=>(x+y+z)/x+(x+y+z)/y+(x+y+z)/z>9
=>y/x+z/x+x/y+z/y+x/z+y/z>6
=>(y/x+x/y)+(z/x+x/z)+(y/z+z/y)>6.
因為y/x+x/y>2,z/x+x/z>2,y/z+z/y>2.所以上式顯然成立.
求某些函數最值
例:求函數的最大值。
函數的定義域為[5,9],y>0
函數僅在,即x=6.44時取到。
柯西簡介
柯西1789年8月2l日出生生于巴黎,柯西是一位多産的數學家,他的全集從1882年開始出版到1974年才出齊最後一卷,總計28卷。著作有《代數分析教程》、《無窮小分析教程概要》和《微積分在幾何中應用教程》。這些工作為微積分奠定了基礎,促進了數學的發展,成為數學教程的典範。
他在純數學和應用數學的功底是相當深厚的,很多數學的定理、公式都以他的名字來稱呼,如柯西不等式、柯西積分公式。在數學寫作上,他被認為在數量上僅次于歐拉的人,他一生一共著作了789篇論文和幾本書,以《分析教程》(1821年)和《關于定積分理論的報告》(1827年)最為著名。不過并不是他所有的創作質量都很高,因此他還曾被人批評“高産而輕率”,這點倒是與數學王子相反。
據說,法國科學院《會刊》創刊的時候,由于柯西的作品實在太多,以緻于科學院要負擔很大的印刷費用,超出科學院的預算,因此,科學院後來規定論文最長的隻能夠到四頁。柯西較長的論文因而隻得投稿到其它地方。
柯西在代數學、幾何學、誤差理論以及天體力學、光學、彈性力學諸方面都有出色的工作。特别是,他弄清了彈性理論的基本數學結構,為力學奠定了嚴格的理論基礎。