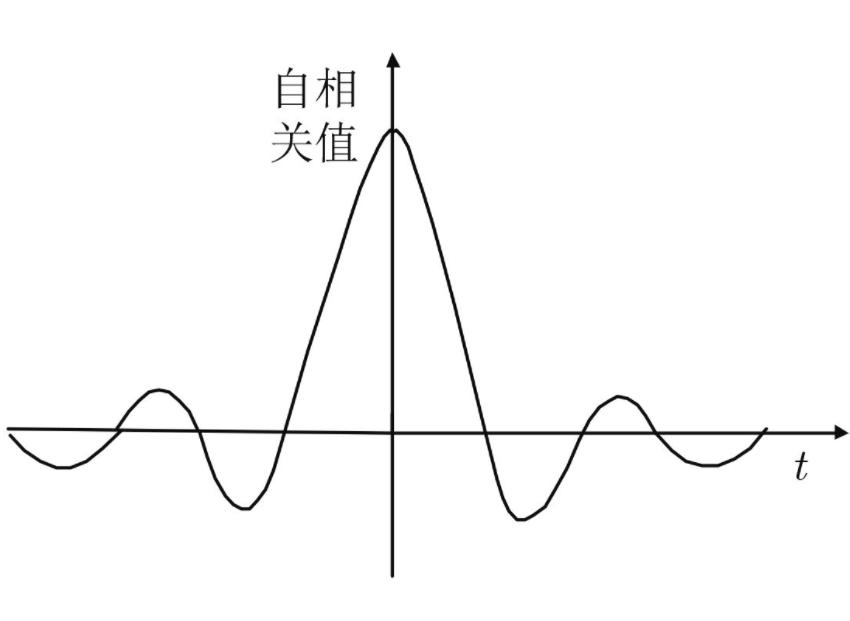
性質
以下以一維自相關函數為例說明其性質,多維的情況可方便地從一維情況推廣得到。
對稱性:從定義顯然可以看出R(i)=R(−i)。連續型自相關函數為偶函數.
當f為實函數時,有:
R_f(-tau)=R_f(tau)。
當f是複函數時,該自相關函數是厄米函數,滿足:
R_f(-tau)=R_f^*(tau)。
其中星号表示共轭。
連續型實自相關函數的峰值在原點取得,即對于任何延時τ,均有|R_f(tau)| leq R_f(0)。該結論可直接有柯西-施瓦茲不等式得到。離散型自相關函數亦有此結論。
周期函數的自相關函數是具有與原函數相同周期的函數。
兩個相互無關的函數(即對于所有τ,兩函數的互相關均為0)之和的自相關函數等于各自自相關函數之和。
由于自相關函數是一種特殊的互相關函數,所以它具有後者的所有性質。
連續時間白噪聲信号的自相關函數是一個δ函數,在除τ=0之外的所有點均為0。
維納-辛欽定理(Wiener–Khinchin theorem)表明,自相關函數和功率譜密度函數是一對傅裡葉變換對:
R(tau)=int_{-infty}^infty S(f) e^{j 2 pi f tau} , df。
S(f)=int_{-infty}^infty R(tau) e^{- j 2 pi f tau} , dtau。
實值、對稱的自相關函數具有實對稱的變換函數,因此此時維納-辛欽定理中的複指數項可以寫成如下的馀弦形式:
R(tau)=int_{-infty}^infty S(f) cos(2 pi f tau) , df。
S(f)=int_{-infty}^infty R(tau) cos(2 pi f tau) , dtau。
舉例
白噪聲的自相關函數為δ函數:
r_{nn}=mathbb{E} { n(t) n(t-tau) }=delta ( tau )。