概念
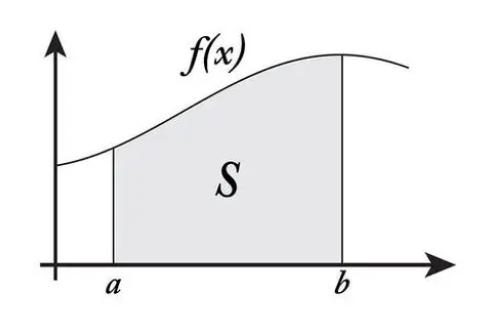
對于一在區間上之給定非負函數,我們想要确定所代表的曲線與坐标軸所夾圖形的面積,我們可以将此記為
黎曼積分的核心思想就是試圖通過無限逼近來确定這個積分值。同時請注意,如取負值,則相應的面積值亦取負值。
定義
1.區間的分割
一個閉區間[a,b]的一個分割P是指在此區間中取一個有限的點列。每個閉區間叫做一個子區間。定義為這些子區間長度的最大值:,其中。
再定義取樣分割。一個閉區間[a,b]的一個取樣分割是指在進行分割後,于每一個子區間中取出一點。的定義同上。
精細化分割:設以及構成了閉區間[a,b]的一個取樣分割,和是另一個分割。如果對于任意,都存在使得,并存在使得,那麼就把分割:、稱作分割、的一個精細化分割。簡單來說,就是說後一個分割是在前一個分割的基礎上添加一些分點和标記。
于是我們可以在此區間的所有取樣分割中定義一個偏序關系,稱作“精細”。如果一個分割是另外一個分割的精細化分割,就說前者比後者更“精細”。
2.黎曼和
對一個在閉區間[a,b]有定義的實值函數,關于取樣分割、的黎曼和定義為以下和式:
式中的每一項是子區間長度與在處的函數值的乘積。直觀地說,就是以标記點到X軸的距離為高,以分割的子區間為長的矩形的面積。
(一列黎曼和。右上角的數字表示矩形面積總和。這列黎曼和趨于一個定值,記為此函數的黎曼積分。)
3.黎曼積分
不太嚴格地來說,黎曼積分就是當分割越來越“精細”的時候,黎曼和趨向的極限。下面的證明中,會對“越來越‘精細’”作出嚴格的定義。
要使得“越來越‘精細’”有效,需要把趨于0。如此中的函數值才會與接近,矩形面積的和與“曲線下方”的面積的差也會越來越小。實際上,這就是黎曼積分定義的大概描述。
嚴格定義如下:
是函數在閉區間[a,b]上的黎曼積分,當且僅當對于任意的,都存在,使得對于任意的取樣分割、,隻要它的子區間長度最大值,就有:
也就是說,對于一個函數,如果在閉區間[a,b]上,無論怎樣進行取樣分割,隻要它的子區間長度最大值足夠小,函數的黎曼和都會趨向于一個确定的值,那麼在閉區間[a,b]上的黎曼積分存在,并且定義為黎曼和的極限,這時候稱函數為黎曼可積的。
這個定義的缺陷是沒有可操作性,因為要檢驗所有的取樣分割是難以做到的。下面引進另一個定義,然後證明它們是等價的。
另一個定義:
是函數在閉區間[a,b]上的黎曼積分,當且僅當對于任意的,都存在一個取樣分割、,使得對于任何比其“精細”的分割和,都有:
這兩個定義是等價的。如果有一個滿足了其中一個定義,那麼它也滿足另一個。首先,如果有一個滿足第一個定義,那麼隻需要在子區間長度最大值的分割中任取一個。對于比其精細的分割,子區間長度最大值顯然也會小于,于是滿足
黎曼積分通常被定義為達布積分(即第二個定義),因為達布積分比黎曼積分更簡單、更有可操作性。
性質
1.線性
黎曼積分是線性變換,也就是說,如果和在區間[a,b]上黎曼可積,和是常數,則:
由于一個函數的黎曼積分是一個實數,因此在固定了一個區間[a,b]後,将一個黎曼可積的函數設到其黎曼積分的映射是所有黎曼可積的函數空間上的一個線性泛函。
2.正定性
如果函數在區間[a,b]上幾乎處處(勒貝格測度意義上)大于等于0,那麼它在[a,b]上的積分也大于等于零。如果在區間[a,b]上幾乎處處大于等于0,并且它在上的積分等于0,那麼幾乎處處為0。
3.可加性
如果函數在區間[a,c]和[c,b]上都可積,那麼在區間[a,b]上也可積,并且有
無論a、b、c之間的大小關系如何,以上關系式都成立。
4.其他性質
(1)[a,b]上的實函數是黎曼可積的,當且僅當它是有界和幾乎處處連續的。
(2)如果[a,b]上的實函數是黎曼可積的,則它是勒貝格可積的。
(3)如果是[a,b]上的一個一緻收斂序列,其極限為,那麼:
(4)如果一個實函數在區間上是單調的,則它是黎曼可積的,因為其中不連續的點集是可數集。
推廣
黎曼積分可推廣到值屬于維空間的函數。積分是線性定義的,特别地,由于複數是實數向量空間,故值為複數的函數也可定義積分。
黎曼積分隻定義在有界區間上,擴展到無界區間并不方便。可能最簡單的擴展是通過極限來定義積分,即如同反常積分(improper integral)一樣。
不幸的是,這并不是很合适。平移不變性(如果把一個函數向左或向右平移,它的黎曼積分應該保持不變)喪失了。一般要求積分存在且與積分順序無關。即使這滿足,依然不是我們想要的,因為黎曼積分與一緻極限不再具有可交換性。例如,令在上,其它域上等于0。對所有。但一緻收斂于0,因此的積分是0。因此。即使這是正确的值,可看出對于極限與普通積分可交換的重要準則對反常積分不适用。這限制了黎曼積分的應用。
一個更好的途徑是抛棄黎曼積分而采用勒貝格積分。雖然勒貝格積分是黎曼積分的擴展這點看上去并不是顯而易見,但不難證明每個黎曼可積函數都是勒貝格可積的,并且當二者都有定義時積分值也是一緻的。
事實上黎曼積分的一個直接擴展是Henstock–Kurzweil積分。
擴展黎曼積分的另一種途徑是替換黎曼累加定義中的因子,粗略地說,這給出另一種意義上長度間距的積分。這是黎曼-斯蒂爾切斯積分所采用的方法