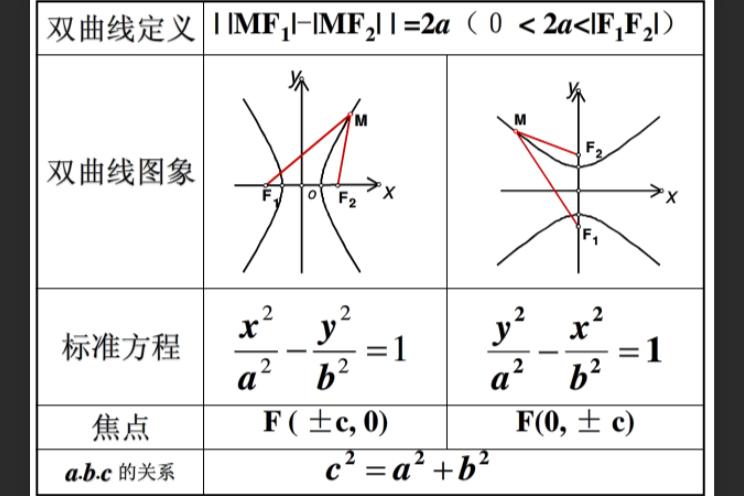
定義
設雙曲線的焦距為2c,雙曲線上任意一點到焦點F1,F2的距離的差的絕對值等于常數2a(c>a>0)
以F1,F2所在直線為x軸,線段F1F2的垂直平分線為y軸,建立直角坐标系xOy,則F1,F2的坐标分别為(-c,0),(c,0)
設M(x,y)為雙曲線上任意一點,根據雙曲線定義知
|MF1-MF2|=2a
即||=2a
化簡得
因為
所以令(b>0)得:
兩邊除以得(a>0,b>0即焦點在x軸上)
類似可以得到焦點為F1(0,-c),F2(0,c)的雙曲線的方程(a>0,b>0即焦點在y軸上)
以上兩種方程都叫做雙曲線的标準方程。
方程推導
橢圓和雙曲線标準方程的推導方法大緻有兩種:一種是教材上移項平方的方法,另一種是資料上常見的構造對偶式的方法.這兩種方法的運算量都比較大,尤其前一種方法需要兩次移項平方.最近,筆者在進行橢圓的教學時,又發現了一種運算量較小的辦法,即根據圓和橢圓的方程都具備“二元二次”的特征,可通過構造圓的方程能簡化橢圓标準方程的推導過程,而該方法也同樣适用于雙曲線标準方程的推導。