上界

簡介

上界，是與偏序集有關的一個特殊元素。指偏序集中大于或等于它的子集中一切元素的元素。設是偏序集，，若對所有都有xRa，則a稱為B在偏序集中的上界，簡稱B的上界，記為。若a是B的上界，對于B的任何上界c，都有aRc，則a稱為B的上确界（或最小上界），記為。

定義

考慮一個實數集合M。如果有一個實數s，使得M中任何數都不超過s，那麼就稱s是M的一個上界。

用數學符号表示為：對∀x∈M，都有x≤s，則稱s是M的上界（upper bound）。

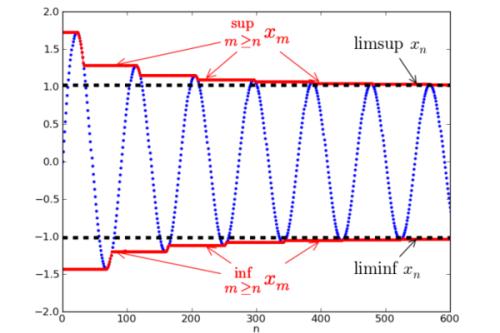
确界原理：若R的子集M有上界，則必有上确界；若集合M有下界，則必有下确界。

上确界定義：設S是R中的一個數集，若數η∈R滿足

（i）對∀x∈S，有η≥x，即η是S的上界；

（ii）對∀a<η,存在x0∈S，使得x0>a，即η是S的最小上界（least upper bound），則稱η為數集S的上确界；

下确界定義：設S是R的一個數集，若數ξ∈R滿足：

（i）對∀x∈S，有ξ≤x，即ξ是S的下界；

（ii）對∀β>ξ,∃x0∈S，使得x0<β，即ξ是S的最大下界（greatest lower bound），則稱ξ為數集的S的下确界；

由戴德金定理證明非空有上界數集必有上确界，非空有下界數集必有下确界同理。

設S為一非空有上界數集，即成立。取數集B為S所有上界的集合，A=R/B。則：

①由取法可知，故。，故，因此。

②。

③∵A中任何元素都不是S的上界，∴。

又∵B中任何元素都是S的上界，∴。

故必有。

∴由戴德金定理可知，要麼A中有最大值，要麼B中有最小值。設這個值為η，并且，恒成立。

假設η是A中的最大值，即，那麼，。

又∵。

但，，與B中任何元素都是S的上界矛盾。

∴η是B中的最小值，即S有最小上界（上确界）。

舉例

對一個，它的上界可能不存在，或可能不止一個。例如，令A={1,2,3}，R={|a整除b}。當B1={2,3}時，B1沒有上界，當B2={1}時，有上界1,2,3，且1是B2的上确界。

對，若上确界存在，則是惟一的。一個子集B有上界時它未必有上确界，有上确界也不一定在子集B之中，例如，如概述圖中哈塞圖表示的以A={a，b，c，d，e}為基本集的一個偏序集，子集B={b，c，d}，以a為上界，a{b，c，d}。子集{e，f}的上界與上确界都是f。子集{c，d，e}無上界，也無上确界。

非空的完全有序集的每個有限子集都有上界和下界。

例如，5是集合{5，8，42，34，13934}的下界。

另一個例子是對于集合{42}，數字42既是上界和下界，所有其他實數都不是該集合的上限或下限。

所有自然數的每個子集都具有下界，因為自然數具有最小元素（0或1，取決于自然數的确切定義）。自然數的無限子集不能從上面界定。整數的無限子集可以從下方界定或從上方界定。有理數字的無限子集可能來自也可能不會從下方界定，也可能不限于上述。