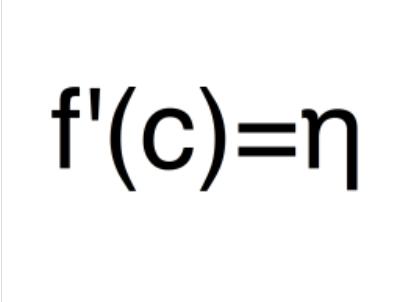達布中值定理:數學定理-中文百科頻道

定理定義

微分達布定理表明區間内的導函數具有介值性，這使得我們在考慮一些數學分析問題時，往往可以不需要最高階導函數的連續性。而在微分方程理論中，比較定理的思想對于解的估計非常重要。

數學表達形式

設y=f(x)在(A，B)區間中可導，且[a，b]包含于(A，B)，，則對于任意給定的η：f'(a)<η使得f'(c)=η。

等價形式

設f(x)在上可微，若在上f′(x)不等于0 ，則f′(x)在上保持定号(恒正或恒負)。

其它表達形式

若函數f(x)在上可導，則f′(x)在上可取f′(a)和f′(b)之間任何值。

驗證推導

方法1

已知f'(a)<η。

若g(a)=g(b)，則由羅爾中值定理：存在ε∈(a，b)使。

不妨設g(a)>g(b)，又g'(b)>0，由極限保号性，存在使。

由介值定理存在ζ∈(a，ξ)使。

又由羅爾中值定理，存在δ∈(ζ，b)使。

所以無論如何總存在x∈(a，b)使g'(x)=0即。

方法2

構造函數。

由于f(x)在(a，b)區間内可導，所以f(x)在(a，b)區間内連續，故g(x)在(a，b)區間内連續。

補充定義使得g(x)在x=a，x=b處連續。

因為，所以一定存在x>a，使得，

即x=a不是函數g(x)在[a，b]上的最小值，同理x=b也不是函數g(x)在[a，b]上的最小值，

故g(x)在(a，b)區間内取得最小值，

所以必然存在ξ∈(a，b)，使（費馬定理），

所以對于任意給定的η，都存在一點c∈(a，b)使得

方法3

引理1若f(x)于〔a，， b〕上連續，f(a)=f(b)，則存在α，β∈(a，b)，使f(α)=f()證明若f(x')=f(a)，x ∈(a，b)，顯然，結論成立。否則，存在c∈(a，b)，

，

不妨設fc)>f(a)，則

因為f(x)在〔a，c〕上連續，由閉區間上連續函數的介值性，存在α∈(a，c)，使

同理︰存在β∈(c，b)，使

且 a，β∈(a，b)、證畢。

定理推廣

微分中值定理的一種證明，微分達布定理表明區間内的導函數具有介值性，這使得我們在考慮一些數學分析問題時，往往可以不需要最高階導函數的連續性。而在微分方程理論中，比較定理的思想對于解的估計非常重要。

在數學分析的教學中，中值定理類問題是一個難點，利用微分達布定理并引入比較定理的思想，不僅給學生們提供了解決此類問題的統一方法，提高了學習效率，更提高了學生的認識，是值得嘗試的。筆者對此作了初步的讨論，讀者可進一步參看文獻。本文則是對相關讨論的進一步完善。因此我們引入了布達定理：

定理A設實函數f(x)在[a，b]上點點可導，，則存在夫∈(a，b)使得

讀者可以在數學分析的很多教材中找到這一定理，例如，教材[4一7]。通常，數學分析教材對于如何應用達布定理着墨不多，在[4，7]中，它僅以習題的形式出現。

達布定理表明，區間上點點可導的函數，其導函數具有介值性。該定理的一個直接推論是，若f(z)在某區間上點點可導且導數不為零，在該區間恒正或恒負。

我們将會看到，達布定理使得我們在讨論微分中值定理類問題時，通常隻需要假設最高階導數點點存在，而不必假設其連續。

發展簡史

高數課程講微分中值定理時，比較強調拉格朗日定理。從理論體系講，這是對的，然而從解題角度，卻是羅爾定理用得更多。以07年的考研試卷中的一道難題為例：

證明令p(x) = f(x)-gr)，則o(a)= p(b)=0。要用羅爾定理隻要找y(x)在( a，b)内一個零點。先排除一特殊情形：f(x)、g(x)在(ab)内同一點達到最大值，于是p(x）=0。分别在[ a，r]、[r，b]上對p(x)用羅爾定理知存在∈ (a，x)5e (x，b)使，再在[56]上對p'(x)用羅爾定理便知存在f ∈(5i5)C(a，b)使p"(E)=0，這便是題目所要證明的結果。