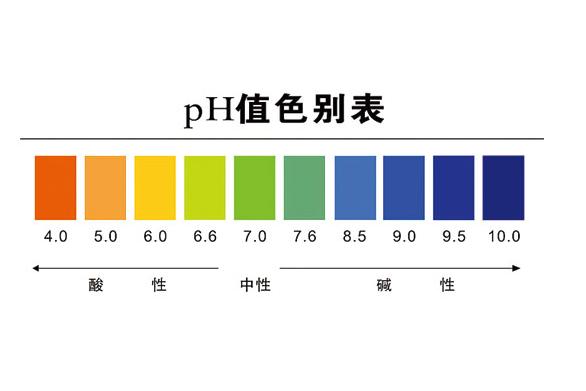
發展簡史
人們對拉格朗日中值定理的認識可以上溯到公元前古希臘時代。古希臘數學家在幾何研究中得到如下結論:“過抛物線弓形的頂點的切線必平行于抛物線弓形的底”。這正是拉格朗日定理的特殊情況,古希臘數學家阿基米德正是巧妙地利用這一結論,求出抛物弓形的面積.。
意大利卡瓦列裡在《不可分量幾何學》(1635年)的卷一中給出處理平面和立體圖形切線的有趣引理,其中引理3基于幾何的觀點也叙述了同樣一個事實:曲線段上必有一點的切線平行于曲線的弦。這是幾何形式的微分中值定理,被人們稱為卡瓦列裡定理。該定理是拉格朗日中值定理在幾何學中的表達形式。
1797年,法國數學家拉格朗日在《解析函數論》一書中首先給出了拉格朗日定理,他給出的定理的最初形式是:“函數
在與之間連續,在與之間有最小值與最大值,則必取與之間的一個值。”拉格朗日給出最初的證明,但證明并不嚴格,他給的條件比現在的條件要強,他要求函數f(x)在閉區間上具有連續導數,并且他所用的連續也是直觀的,而不是抽象的。
十九世紀初,在微積分嚴格化運動中,柯西給出了拉格朗日中值定理的嚴格證明,在《無窮小計算教程概論》中,柯西證明了”如果導數在閉區間[a,b]上連續,則必存在一點,使得。 ”柯西又在《微分計算教程》中将拉格朗日中值定理推廣為柯西中值定理。
現代形式的拉格朗日中值定理是由法國數學家博(O.Bonnet)給出的,他不是利用導數的連續性,而是利用羅爾定理對拉格朗日中值定理進行了重新證明。
定理定義
設在上可積,若函數在上單調遞減,且,則至少存在一點,使得
驗證推導
這個定理的推導比較複雜,脌扯到積分上限函數:。以下用 表示從 到 的定積分。
首先需要證明,若函數在 内可積分,則 在此區間内為一連續函數。
證明: 設, 則
因 在上不變号,則由積分第一中值定理知,在 上至少存在一點 , 使得
于是,有
即 , 得證。
定理推廣
1、定理的直接應用
例1設在上可積,在上單調遞增且非負,在處連續,那麼在上存在使
證明:令, ,因為非負且單調遞減( )利用公式有
,而,即
2、積分第二中值定理在證明不等式中的應用
例2證明時,
證明:取,由積分中值定理和它的推論可得:
3、積分中值定理在極限中的應用
例3證明極限
證明:由積分中值定理和它的推論可得:令
令可知g(x)在[0,1]上連續,而且不變号。所以存在ξ使得,因此有以下式子
定理意義
積分第二中值定理證明了在一個二元函數表示的曲頂柱體中,必然存在一個介于最高點和最低點的點,過該點可以做一個與底面平行的平面,截曲頂柱體側面形成的柱體體積和原來的曲頂柱體體積相等。