别稱
擺線是指一個圓在一條定直線上滾動時,圓周上一個定點的軌迹,又稱圓滾線、旋輪線。
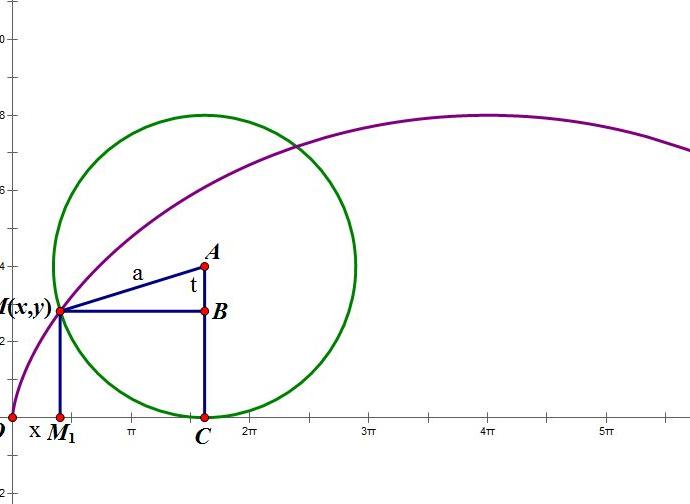
圓上定點的初始位置為坐标原點,定直線為x軸。當圓滾動j 角以後,圓上定點從 O 點位置到達P點位置。當圓滾動一周,即 j從O變動2π時,動圓上定點描畫出擺線的第一拱。再向前滾動一周, 動圓上定點描畫出第二拱,繼續滾動,可得第三拱,第四拱……,所有這些拱的形狀都是完全相同的 ,每一拱的拱高為2a(即圓的直徑),拱寬為2πa(即圓的周長)。
性質
到17 世紀,人們發現擺線具有如下性質:
1.它的長度等于旋轉圓直徑的 4 倍。尤為令人感興趣的是,它的長度是 一個不依賴于π的有理數。
2.在弧線下的面積,是旋轉圓面積的三倍。
3.圓上描出擺線的那個點,具有不同的速度——事實上,在特定的地方它甚至是靜止的。
4.當彈子從一個擺線形狀的容器的不同點放開時,它們會同時到達底部。
方程式
x=r*(t-sint); y=r*(1-cost)r為圓的半徑, t是圓的半徑所經過的弧度(滾動角),當t由0變到2π時,動點就畫出了擺線的一支,稱為一拱。
曆史
擺線最早出現可見于公元 1501 年出版的 C·鮑威爾的一本書中.但在 17 世 紀,大批卓越的數學家(如伽利略,帕斯卡,托裡拆利,笛卡兒,費爾馬, 伍任,瓦裡斯,惠更斯,約翰·伯努利,萊布尼茲,牛頓等等)熱心于研究這一曲線的性質.17 世紀是人們對數學力學和數學運動學愛好的年代,這能解釋人們為什麼對擺線懷有強烈的興趣。在這一時期,伴随着許多發現,也出現了衆多有關發現權的争議,剽竊的指責,以及抹煞他人工作的現象。這樣,作為一種結果,擺線被貼上了引發争議的“金蘋果”和“幾何的海倫” 的标簽。
擺線的研究最初開始于庫薩的尼古拉,之後馬蘭·梅森也有針對擺線的研究。1599年伽利略為擺線命名。1634年吉勒斯·德·羅貝瓦勒指出擺線下方的面積是生成它的圓面積的三倍。1658年克裡斯多佛·雷恩也向人們指出擺線的長度是生成它的圓直徑的四倍。在這一時期,伴随着許多發現,也出現了衆多有關發現權的争議,甚至抹殺他人工作的現象,而因此擺線也被人們稱作“幾何學中的海倫”(The Helen of Geometers)。
相關故事
時鐘
時鐘已變成現代人不可或少的必備工具之一,沒有時鐘,人們将不知時間,許多重要的約會便會錯過,當各位在看表的時候,不知可曾想過,時鐘裡面隐藏了些甚麼道理,一砂一世界,許多我們視為理所當然的事都是先民流血流汗一點一滴累積而成的。
在時鐘裡面到底隐藏了什麼東西 将這些理論寫出來可是厚厚的一大本呢!回想以前的中世紀航海時代,時間的掌握是關乎全船人生命安危的大事,想要和大海搏鬥,時間是不可或缺的因素,古時候是以沙漏水鐘來計時,但這些計時工具相當不準确,為了增加船員生存的機會,發明精确的計時器變成了當時科學界的當務之急。
那時在意大利有一位年輕的科學家伽利略,有一次在比薩斜塔處意外地發現一個有趣的現象,教堂的吊燈來回擺動時,不管擺動的幅度大還是小,每擺動一次用的時間都相等。當時,他是以自己的心跳脈搏來計算時間的.從此以後,伽利略便廢寝忘食的研究起物理和數學來,他曾用自行制的滴漏來重新做單擺的試驗,結果證明了單擺擺動的時間跟擺幅沒有關系,隻跟單擺擺線的長度有關.這個現象使伽利略想到或許可以利用單擺來制作精确的時鐘,但他始終并沒有将理想付之實行。
伽利略的發現振奮了科學界,可是不久便發現單擺的擺動周期也不完全相等。原來,伽利略的觀察和實驗還不夠精确.實際上,擺的擺幅愈大,擺動周期就愈長,隻不過這種周期的變化是很小的。所以,如果用這種擺來制作時鐘,擺的振幅會因為摩擦和空氣阻力而愈來愈小,時鐘也因此愈走愈快。
過了不久,荷蘭科學家惠更斯決定要做出一個精确的時鐘來.伽利略的單擺是在一段圓弧上擺動的,所以我們也叫做圓周擺。惠更斯想要找出一條曲線,使擺沿著這樣的曲線擺動時,擺動周期完全與擺幅無關,這群科學家放棄了物理實驗,純粹往數學曲線上去研究,經過不少次的失敗,這樣的曲線終於找到了,數學上把這種曲線叫做“擺線”,“等時曲線”或“旋輪線”。
動手驗證
如果你用硬紙闆剪一個圓,在圓的邊緣固定一枝鉛筆,當這圓沿一條直線滾動時,鉛筆便會畫出一條擺線來.相信這樣的玩具許多人都已經看過玩過,以前的街上,常會看到街邊小販在兜售這種擺線玩具,許多人贊歎擺線的美麗,但卻不知擺線與時鐘的相關性.鐘表店裡面那些有鐘擺的時鐘,都是利用擺線性質制作出來的.由于擺線的發現,使得精确時鐘的制作不是夢想.這也使人類科技向前邁進一大步。
基本原理
擺線針輪行星傳動中,擺線輪齒廓曲線運用内齧合發生圓産生的短幅外擺線。
有一發生圓(滾圓)半徑為rp',基圓半徑為rc',基圓内切于發生圓,當發生圓繞基圓作純滾動,其圓心Op分别處于Op1、Op2、Op3、Op4、Op5、Op6......各位置時,由此固結在發生圓平面上的點M分别經過M1、M2、M3、M4、M5、M6......各位置,由此發生圓周期滾動,發生圓上點M所形成的軌迹曲線即為短幅外擺線。
由以上擺線生成的幾何關系 若仍保持以上的内切滾動關系,将基圓和擺線視為剛體相對于發生圓運動,則形成了擺線圖形相對發生圓圓心Op作行星方式的運動,這就是行星擺線傳動機構的基本原理。
最速降線
在一個斜面上,擺兩條軌道,一條是直線,一條是曲線,起點高度以及終點高度都相同。兩個質量、大小一樣的小球同時從起點向下滑落,曲線的小球反而先到終點。這是由于曲線軌道上的小球先達到最高速度,所以先到達。然而,兩點之間的直線隻有一條,曲線卻有無數條,那麼,哪一條才是最快的呢?伽利略于1630年提出了這個問題,當時他認為這條線應該是一條弧線,可是後來人們發現這個答案是錯誤的。
1696年,瑞士數學家約翰·伯努利解決了這個問題,他還拿這個問題向其他數學家提出了公開挑戰。牛頓、萊布尼茲、洛比達以及雅克布·伯努利等解決了這個問題。這條最速降線就是一條擺線,也叫旋輪線。
意大利科學家伽利略在1630年提出一個分析學的基本問題——“一個質點在重力作用下,從一個給定點到不在它垂直下方的另一點,如果不計摩擦力,問沿着什麼曲線滑下所需時間最短。”。他說這曲線是圓,可是這是一個錯誤的答案。
瑞士數學家約翰.伯努利在1696年再提出這個最速降線的問題(problem of brachistochrone),征求解答。次年已有多位數學家得到正确答案,其中包括牛頓、萊布尼茲、洛必達和伯努利家族的成員。這問題的正确答案是連接兩個點上凹的唯一一段旋輪線。
旋輪線與1673年荷蘭科學家惠更斯讨論的擺線相同。因為鐘表擺錘作一次完全擺動所用的時間相等,所以擺線(旋輪線)又稱等時曲線。
看Johann Bernoulli 對最速降線問題的beautiful解答:
如果使分成的層數n無限地增加,即每層的厚度無限地變薄,則質點的運動便趨于空間A、B兩點間質點運動的真實情況,此時折線也就無限增多,其形狀就趨近我們所要求的曲線——最速降線.而折線的每一段趨向于曲線的切線,因而得出最速降線的一個重要性質:任意一點上切線和鉛垂線所成的角度的正弦與該點落下的高度的平方根的比是常數.而具有這種性質的曲線就是擺線.所謂擺線,它是一個圓沿着一條直線滾動(無滑動)時,圓周上任意一點的軌迹。
因此,最速降線就是擺線,隻不過在最速降線問題中,這條擺線是上、下颠倒過來的罷了.
以上便是Johann Bernoulli當時所給最速降線問題的解答.當然,這個解答在理論上并不算十分嚴謹的.但是,這個解答所蘊含的基本觀點的發展,導緻了一門新的學科——變分學.最速降線問題的最終而完備的解答,需要用到變分學的知識.
證明式
過原點半徑為r的擺線參數方程為
在這裡實參數t是在弧度制下,圓滾動的角度。對每一個給出的t,圓心的坐标為(rt, r)。 通過替換解出t可以求的笛卡爾坐标方程為
擺線的第一道拱由參數t在(0, 2π)區間内的點組成。
擺線也滿足下面的微分方程。
面積
一條由半徑為r的圓所生成的拱形面積可以由下面的參數方程界定:
微分,
于是可以求得
弧長
弧形的長度可以由下面的式子計算出: