基本概念
定義
設函數 ,式中 隻對 在非負整數值上有定義,在自變量x依次取遍非負整數,即 時,相應的函數值為
簡記為
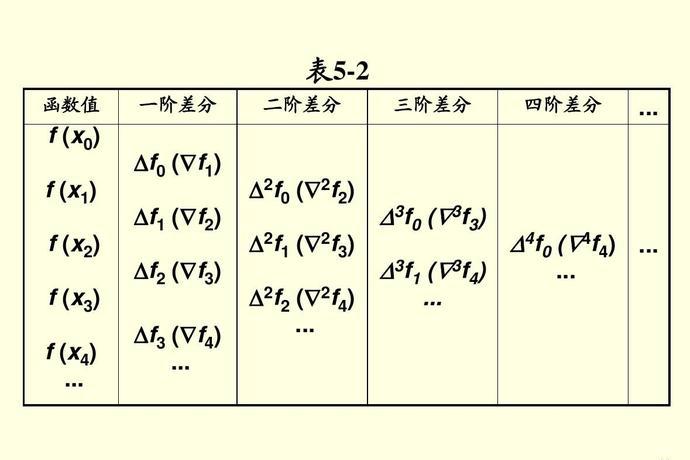
定義1 當自變量從 變到 時,函數 的改變量
稱為函數 在點 的一階差分,通常記作
例題解析
例1 設 ,求 。
解: 。
例2 設 (其中 且 ),求 。
解: 。
可見,指數函數的差分等于指數函數乘上一個常數。
例3 設 ,求 。
解:。
高階差分
下面給出高階差分的定義。
定義2 當自變量從 變到 時,一階差分的差分
稱為函數 的二階差分,記作 ,即
同樣,二階差分的差分稱為三階差分,記為 ,即
依此類推,可得函數的n階差分為
性質及定理
(1)(C為常數);
(2);
(3);
(4)若為最高次項系數為的n次多項式,則;
(5)若為n次多項式,則;
(6)若,則是x的一個次數小于等于r的代數多項式。
差分方程
定義3 凡含有自變量x,未知函數 及未知函數的差分 的函數方程稱為差分方程,如方程
是差分方程.方程中差分的最高階數(即△上方最大的數字)稱為差分方程的階,幾階就稱為幾階差分方程,n階稱為n階差分方程。
由于n階差分總可表示成n+1個點上函數值的線性組合.因而差分方程又可定義如下。
定義4 凡是含有自變量x以及兩個或兩個以上的未知函數值的函數方程
稱為差分方程。方程中未知函數下标的最大值與最小值的差稱為差分方程的階。
定義5 (1) 如果将已知函數 代人差分方程,能使其對 成為恒等式,則稱函數 為該差分方程的一個解;
(2) 對于n階差分方程,含有n個獨立的任意常數的解稱為該差分方程的通解;(3)差分方程的不包含任意常數的解稱為該方程的特解。
在通解中給定一組任意常數所确定的解,就是該n階差分方程的特解,常由初始條件求出一組任意常數的值,确定特解。