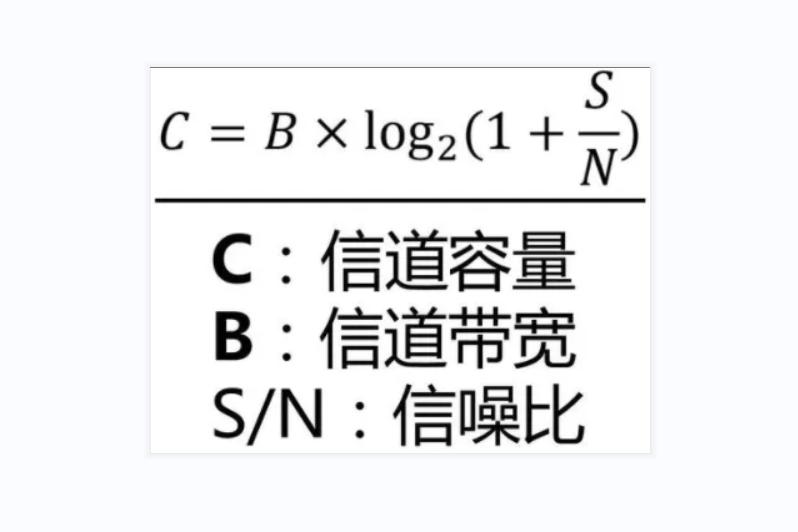
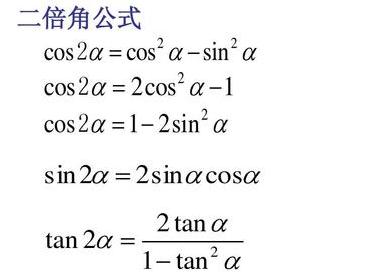解析
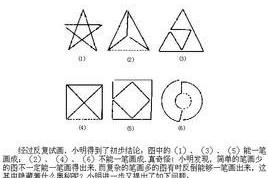
衆所周知的"哥尼斯堡城'七橋問題'"被大數學家歐拉開創了數學新分支-----圖論。也就是"一筆畫"。一筆畫圖形的必要條件是:奇點數目是0或者2。圖⑴的"七橋問題"A,B,C,D都是奇節點,數目是4,所以不能夠"一筆畫"。我們把節點轉換回來,成為"節面"(區域),來考慮"一筆畫"。
一,在平面中,4個或者4個以下的區域可以構成兩兩相連的區域,可以一筆畫。圖⑵。每個區域必須是單連通的,就是一個區域不能夠是分成2塊或者2塊以上。圖⑶就不是單連通的。這是著名的四色猜想。大家知道,平面上不可能有兩兩相同的5個區域。
二,緊緻封閉平面,在一個輪胎狀的表面,7個或者7個以下的區域可以構成兩兩相連的區域。可以"一筆劃"。把圖(A)上下對折以後,再左右對折,形成一個輪胎狀,7個區域兩兩相連
上下對折再左右對折成輪胎形狀圖A
上下對折再左右對折成輪胎形狀圖A
(國外數學家給出).兩兩相連的區域可以不經過其它區域到達任何一個區域。P。J希伍德以畢生精力研究四色定理,并且證明了5色定理,稀伍德考察了一般曲面着色問題提出一個推測:在有P>1個洞的封閉曲面上,足以為任何地圖着色的最小數等于(左圖上下對折再左右對折就是一個輪胎,7個區域兩兩相連,可以一筆畫)
Np=[(7+√(48p))/2],其中[X]表示整數部分,
三個洞的封閉曲面
P=1,M1=7,即圖(A).
克萊因瓶也隻能7色,而不是8色。三,德國數學家G.林格證明了:足以為任何一張有P>1個洞的封閉曲面着色的真正最小色數Np,Np-Mp《2,以後美國數學家VT楊斯進一步證明了Np-Mp《1,而希伍德的假設對于不同球面幾乎一切封閉曲面都是成立的,1974年,林格作出了完整的證明。例如,兩個洞的封閉曲面應該是M2=[7+√(48×2)/2]=8,能夠作8色。(見左圖)王曉明王蕊珂經過9年杜撰。
四,如果我們不限定形态
三個洞的封閉曲面M三個3=[7+√(48×3)/2]=9,能夠作9色四個洞10個區域兩兩相連一筆畫
五,圖D.這是有4個洞的10個兩兩相連區域圖,下面四叉按照ABCD對應。
數學家歐拉找到一筆畫的規律是:
⒈凡是由偶點組成的連通圖,一定可以一筆畫成。畫時可以把任一偶點為起點,最後一定能
圖B的平面圖
圖B的平面圖
以這個點為終點畫完此圖。
⒉凡是隻有兩個奇點的連通圖(其餘都為偶點),一定可以一筆畫成。畫時必須把一個奇點為起點,另一個奇點終點。
⒊其他情況的圖都不能一筆畫出。(有偶數個奇點除以二便可算出此圖需幾筆畫成。)
比如附圖:(a)為⑴情況,因此可以一筆畫成;(b)(c)(d)則沒有符合以上兩種情況,所以不能一筆畫成。
相關名詞含義
◎頂點與指數:設一個平面圖形是由有限個點及有限條弧組成的,這些點稱為圖形的頂點,從任一頂點引出的該圖形的弧的條數,稱為這個頂點的指數。
◎奇頂點:指數為奇數的頂點。
◎偶頂點:指數為偶數的頂點
規律證明
先定義能一筆畫出并回到起點的圖為歐拉圖,連通就是說任意兩個節點之間可以找到一條連接它們的線。這個要求看來很重要,直觀方法中與這一點對應的是說原圖本身不能是分成多個的
證明
設G為一歐拉圖,那麼G顯然是連通的。另一方面,由于G本身為一閉路徑,它每經過一個頂點一次,便給這一頂點增加度數2,因而各頂點的度均為該路徑經曆此頂點的次數的兩倍,從而均為偶數。反之,設G連通,且每個頂點的度均為偶數,欲證G為一歐拉圖。為此,對G的邊數歸納。當m=1時,G必定為單結點的環,顯然這時G為歐拉圖。設邊數少于m的連通圖,在頂點度均為偶數時必為歐拉圖,現考慮有m條邊的圖G。設想從G的任一點出發,沿着邊構畫,使筆不離開
圖且不在構畫過的邊上重新構畫。由于每個頂點都是偶數度,筆在進入一個結點後總能離開那個結點,除非筆回到了起點。在筆回到起點時,它構畫出一條閉路徑,記為H。從圖G中删去H的所有邊,所得圖記為G',G'未必連通,但其各頂點的度數仍均為偶數.考慮G的各連通分支,由于它們都連通,頂點度數均為偶數,而邊數均小于m,因此據歸納假設,它們都是歐拉圖。此外,由于G連通,它們都與H共有一個或若幹個公共頂點,因此,它們與H一起構成一個閉路徑。這就是說,G是一個歐拉圖。
折疊一筆畫定理
1736年,歐拉證實:七橋問題的走法根本不存在。同時,他發表了"一筆畫定理":一個圖形要能一筆畫完成必須符合兩個條件,即圖形是封閉聯通的和圖形中的奇點(與奇數條邊相連的點)個數為0或2。
歐拉的研究開創了數學上的新分支――拓撲學的先聲。
歐拉定理
七橋問題和歐拉定理。歐拉通過對七橋問題的研究,不僅圓滿地回答了哥尼斯堡居民提出的問題,而且得到并證明了更為廣泛的有關一筆畫的三條結論,人們通常稱之為歐拉定理。對于一個連通圖,通常把從某結點出發一筆畫成所經過的路線叫做歐拉路。人們又通常把一筆畫成回到出發點的歐拉路叫做歐拉回路。具有歐拉回路的圖叫做歐拉圖。