基本概念
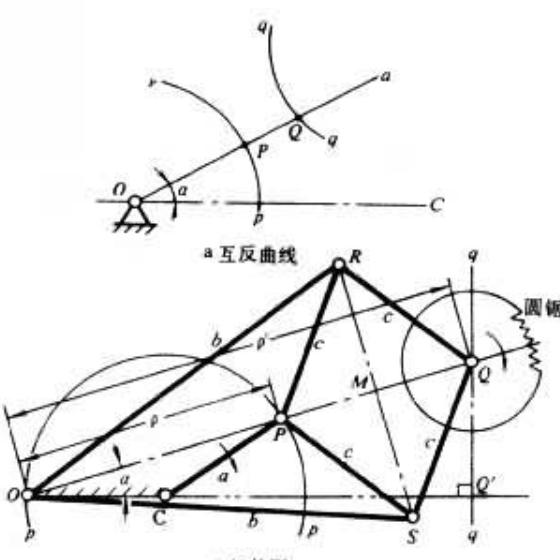
一個彎曲的表面稱為曲面,通常用相應的兩個曲率半徑來描述曲面,即在曲面上某點作垂直于表面的直線,再通過此線作一平面,此平面與曲面的截線為曲線,在該點與曲線相切的圓半徑稱為該曲線的曲率半徑R1。通過表面垂線并垂直于第一個平面再作第二個平面并與曲面相交,可得到第二條截線和它的曲率半徑R2,用R1與R2可表示出液體表面的彎曲情況。若液面是彎曲的,液體内部的壓強p1與液體外的壓強p2就會不同,在液面兩邊就會産生壓強差△P=P1-P2,稱附加壓強,其數值與液面曲率大小有關,可表示為:,式中γ是液體表面張力系數,該公式稱為拉普拉斯方程。
應用環境
數理方程
拉普拉斯方程為:Δu=d^2u/dx^2+d^2u/dy^2=0,其中Δ為拉普拉斯算子,此處的拉普拉斯方程為二階偏微分方程。三維情況下,拉普拉斯方程可由下面的形式描述,問題歸結為求解對實自變量x、y、z二階可微的實函數φ:
其中Δ稱為拉普拉斯算子,拉普拉斯方程的解稱為調和函數。
如果等号右邊是一個給定的函數f(x,y,z),即:
則該方程稱為泊松方程。拉普拉斯方程和泊松方程是最簡單的橢圓型偏微分方程。偏微分算子或Δ(可以在任意維空間中定義這樣的算子)稱為拉普拉斯算子,英文是Laplace operator或簡稱作Laplacian。
狄利克雷問題
拉普拉斯方程的狄利克雷問題可歸結為求解在區域D内定義的函數φ,使得在D的邊界上等于某給定的函數。為方便叙述,以下采用拉普拉斯算子應用的其中一個例子——熱傳導問題作為背景進行介紹:固定區域邊界上的溫度(是邊界上各點位置坐标的函數),直到區域内部熱傳導使溫度分布達到穩定,這個溫度分布場就是相應的狄利克雷問題的解。
諾伊曼邊界條件
拉普拉斯方程的諾伊曼邊界條件不直接給出區域D邊界處的溫度函數φ本身,而是φ沿D的邊界法向的導數。從物理的角度看,這種邊界條件給出的是矢量場的勢分布在區域邊界處的已知效果(對熱傳導問題而言,這種效果便是邊界熱流密度)。
拉普拉斯方程的解
拉普拉斯方程的解稱為調和函數,此函數在方程成立的區域内是解析的。任意兩個函數,如果它們都滿足拉普拉斯方程(或任意線性微分方程),這兩個函數之和(或任意形式的線性組合)同樣滿足前述方程。這種非常有用的性質稱為疊加原理。可以根據該原理将複雜問題的已知簡單特解組合起來,構造适用面更廣的通解。
二維拉普拉斯方程
兩個自變量的拉普拉斯方程具有以下形式:
函數h(x,y為二元函數,h(x,y)對x的二階偏導數+h(x,y)對y的二階偏導數=0
解析函數
解析函數的實部和虛部均滿足拉普拉斯方程。換言之,若z=x+iy,并且
那麼f(z)是解析函數的充要條件是它滿足下列柯西-黎曼方程:f(z)u(x,y)iv(x,y)
u對x的偏導數=v對y的偏導數,u對y的偏導數=-(v對x的偏導數)
上述方程繼續求導就得到
所以u滿足拉普拉斯方程。類似的計算可推得v同樣滿足拉普拉斯方程。
反之,給定一個由解析函數(或至少在某點及其鄰域内解析的函數)f(z)的實部确定的調和函數,若寫成下列形式:
則等式成立就可使得柯西-黎曼方程得到滿足。上述關系無法确定ψ,隻能得到它的微增量表達式:
φ滿足拉普拉斯方程意味着ψ滿足可積條件:
所以可以通過一個線積分來定義ψ。可積條件和斯托克斯定理的滿足說明線積分的結果與積分經過的具體路徑無關,僅由起點和終點決定。于是,我們便通過複變函數方法得到了φ和ψ這一對拉普拉斯方程的解。這樣的解稱為一對共轭調和函數。這種構造解的方法隻在局部(複變函數f(z))的解析域内)有效,或者說,構造函數的積分路徑不能圍繞有f(z)的奇點。譬如,在極坐标平面(r,θ)上定義函數
那麼相應的解析函數為
在這裡需要注意的是,極角θ僅在不包含原點的區域内才是單值的。
拉普拉斯方程與解析函數之間的緊密聯系說明拉普拉斯方程的任何解都無窮階可導(這是解析函數的一個性質),因此可以展開成幂級數形式,至少在不包含奇點的圓域内是如此。這與波動方程的解形成鮮明對照,後者包含任意函數,其中一些的可微分階數是很小的。
幂級數和傅裡葉級數之間存在着密切的關系。如果我們将函數f在複平面上以原點為中心,R為半徑的圓域内展開成幂級數,即
将每一項系數适當地分離出實部和虛部
那麼這便是f的傅裡葉級數。
三維情況
拉普拉斯方程可由下面的形式描述,問題歸結為求解對實自變量x、y、z二階可微的實函數φ:
上面的方程常常簡寫作:
或
其中div表示矢量場的散度(結果是一個标量場),grad表示标量場的梯度(結果是一個矢量場),或者簡寫作:
其中Δ稱為拉普拉斯算子.
拉普拉斯方程的解稱為調和函數。
如果等号右邊是一個給定的函數f(x,y,z),即:
則該方程稱為泊松方程。拉普拉斯方程和泊松方程是最簡單的橢圓型偏微分方程。偏微分算子或Δ(可以在任意維空間中定義這樣的算子)稱為拉普拉斯算子,英文是Laplace operator或簡稱作Laplacian。
拉普拉斯方程的狄利克雷問題可歸結為求解在區域D内定義的函數φ,使得在D的邊界上等于某給定的函數。為方便叙述,以下采用拉普拉斯算子應用的其中一個例子——熱傳導問題作為背景進行介紹:固定區域邊界上的溫度(是邊界上各點位置坐标的函數),直到區域内部熱傳導使溫度分布達到穩定,這個溫度分布場就是相應的狄利克雷問題的解。
拉普拉斯方程的諾伊曼邊界條件不直接給出區域D邊界處的溫度函數φ本身,而是φ沿D的邊界法向的導數。從物理的角度看,這種邊界條件給出的是矢量場的勢分布在區域邊界處的已知效果(對熱傳導問題而言,這種效果便是邊界熱流密度)。
拉普拉斯方程的解稱為調和函數,此函數在方程成立的區域内是解析的。任意兩個函數,如果它們都滿足拉普拉斯方程(或任意線性微分方程),這兩個函數之和(或任意形式的線性組合)同樣滿足前述方程。這種非常有用的性質稱為疊加原理。可以根據該原理将複雜問題的已知簡單特解組合起來,構造适用面更廣的通解。
發明者
拉普拉斯,1749年3月23日生于法國西北部卡爾瓦多斯的博蒙昂諾日,曾任巴黎軍事學院數學教授。1795年任巴黎綜合工科學校教授,後又在高等師範學校任教授。1799年他還擔任過法國經度局局長,并在拿破侖政府中任過6個星期的内政部長。1816年被選為法蘭西學院院士,1817年任該院院長。1827年3月5日卒于巴黎。拉普拉斯在研究天體問題的過程中,創造和發展了許多數學的方法,以他的名字命名的拉普拉斯變換、拉普拉斯定理和拉普拉斯方程,在科學技術的各個領域有着廣泛的應用。
拉普拉斯曾任拿破侖的老師,所以和拿破侖結下不解之緣。拉普拉斯在數學上是個大師,在政治上是個小人物、牆頭草,總是效忠于得勢的一邊,被人看不起,拿破侖曾譏笑他把無窮小量的精神帶到内閣裡。在席卷法國的政治變動中,包括拿破侖的興起和衰落,沒有顯着地打斷他的工作。盡管他是個曾染指政治的人,但他的威望以及他将數學應用于軍事問題的才能保護了他,同時也歸功于他顯示出的一種并不值得佩服的在政治态度方面見風使舵的能力。