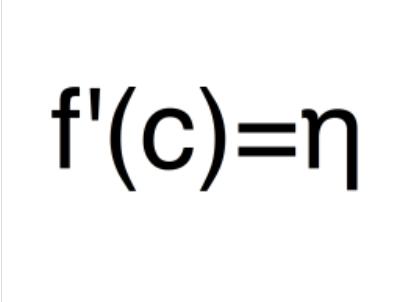达布中值定理:数学定理-中文百科频道

定理定义

微分达布定理表明区间内的导函数具有介值性，这使得我们在考虑一些数学分析问题时，往往可以不需要最高阶导函数的连续性。而在微分方程理论中，比较定理的思想对于解的估计非常重要。

数学表达形式

设y=f(x)在(A，B)区间中可导，且[a，b]包含于(A，B)，，则对于任意给定的η：f'(a)<η使得f'(c)=η。

等价形式

设f(x)在上可微，若在上f′(x)不等于0 ，则f′(x)在上保持定号(恒正或恒负)。

其它表达形式

若函数f(x)在上可导，则f′(x)在上可取f′(a)和f′(b)之间任何值。

验证推导

方法1

已知f'(a)<η。

若g(a)=g(b)，则由罗尔中值定理：存在ε∈(a，b)使。

不妨设g(a)>g(b)，又g'(b)>0，由极限保号性，存在使。

由介值定理存在ζ∈(a，ξ)使。

又由罗尔中值定理，存在δ∈(ζ，b)使。

所以无论如何总存在x∈(a，b)使g'(x)=0即。

方法2

构造函数。

由于f(x)在(a，b)区间内可导，所以f(x)在(a，b)区间内连续，故g(x)在(a，b)区间内连续。

补充定义使得g(x)在x=a，x=b处连续。

因为，所以一定存在x>a，使得，

即x=a不是函数g(x)在[a，b]上的最小值，同理x=b也不是函数g(x)在[a，b]上的最小值，

故g(x)在(a，b)区间内取得最小值，

所以必然存在ξ∈(a，b)，使（费马定理），

所以对于任意给定的η，都存在一点c∈(a，b)使得

方法3

引理1若f(x)于〔a，， b〕上连续，f(a)=f(b)，则存在α，β∈(a，b)，使f(α)=f()证明若f(x')=f(a)，x ∈(a，b)，显然，结论成立。否则，存在c∈(a，b)，

，

不妨设fc)>f(a)，则

因为f(x)在〔a，c〕上连续，由闭区间上连续函数的介值性，存在α∈(a，c)，使

同理︰存在β∈(c，b)，使

且 a，β∈(a，b)、证毕。

定理推广

微分中值定理的一种证明，微分达布定理表明区间内的导函数具有介值性，这使得我们在考虑一些数学分析问题时，往往可以不需要最高阶导函数的连续性。而在微分方程理论中，比较定理的思想对于解的估计非常重要。

在数学分析的教学中，中值定理类问题是一个难点，利用微分达布定理并引入比较定理的思想，不仅给学生们提供了解决此类问题的统一方法，提高了学习效率，更提高了学生的认识，是值得尝试的。笔者对此作了初步的讨论，读者可进一步参看文献。本文则是对相关讨论的进一步完善。因此我们引入了布达定理：

定理A设实函数f(x)在[a，b]上点点可导，，则存在夫∈(a，b)使得

读者可以在数学分析的很多教材中找到这一定理，例如，教材[4一7]。通常，数学分析教材对于如何应用达布定理着墨不多，在[4，7]中，它仅以习题的形式出现。

达布定理表明，区间上点点可导的函数，其导函数具有介值性。该定理的一个直接推论是，若f(z)在某区间上点点可导且导数不为零，在该区间恒正或恒负。

我们将会看到，达布定理使得我们在讨论微分中值定理类问题时，通常只需要假设最高阶导数点点存在，而不必假设其连续。

发展简史

高数课程讲微分中值定理时，比较强调拉格朗日定理。从理论体系讲，这是对的，然而从解题角度，却是罗尔定理用得更多。以07年的考研试卷中的一道难题为例：

证明令p(x) = f(x)-gr)，则o(a)= p(b)=0。要用罗尔定理只要找y(x)在( a，b)内一个零点。先排除一特殊情形：f(x)、g(x)在(ab)内同一点达到最大值，于是p(x）=0。分别在[ a，r]、[r，b]上对p(x)用罗尔定理知存在∈ (a，x)5e (x，b)使，再在[56]上对p'(x)用罗尔定理便知存在f ∈(5i5)C(a，b)使p"(E)=0，这便是题目所要证明的结果。