欧拉示性数

定义

如果一个拓扑空间X有有限的三角剖 h：X→|K|，X的欧拉示性数定义为它的剖分复形K的各个维数单纯形个数（即单纯链复形的秩）的交错和。

对于有限CW-复形(CW-Complex)包括有限单纯复形(simplicial complex)，欧拉示性数可以定义为交错和其中表示维胞腔的个数。

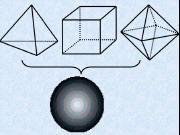
然后，可以把流形的欧拉示性数定义为一个和它同胚的单纯复形的欧拉示性数。例如，圆圈和环面其欧拉示性数为0而实心球欧拉示性数为1。

闭可定向曲面的欧拉示性数可以通过它们的亏格g来计算

闭不可定向曲面的欧拉示性数可以用下式通过它们的(不可定向)亏格k来计算

欧拉示性数和三角化的选择无关。公式也可用于到任意多边形的分解。

对于圆盘，我们有,对于平面我们有,数的时候把外面作为一个面。

对于闭流形，欧拉示性数和欧拉数,也就是其切丛的在流形的基本类上计算的欧拉类。

对于闭黎曼曲面，欧拉示性数也可以通过曲率的积分得到—参看对于二维情况的高斯-博内定理(Gauss-Bonnet)和对于一般情况的广义高斯-博内定理。高斯-博内定理的离散情况的对应是笛卡儿定理，它表明多面体用完整圆圈测量的“总亏量”，是多面体的欧拉示性数；参看亏量。

更一般的，对于所有拓扑空间，我们可以定义第n个贝蒂数作为第n个同调群的阶。欧拉示性数可以定义为如下交换和

这个定义在贝蒂数全都有限并且在一个特定指标以外为0时有意义。

两个同伦的拓扑空间有同构的同调群，所以有相同的欧拉示性数。

从这个定义和庞加莱对偶性，可以得到所有闭合奇数维流形的欧拉数为0的结论。

如果M和N是拓扑空间，则它们的积空间M×N的欧拉示性数为

经典公式

有关欧拉示性数的一个经典的公式是

其中是拓扑空间X的第i个贝蒂数，这一公式称为欧拉-庞加莱公式。该公式亦说明了欧拉示性数不依赖于剖分的选取，是一个拓扑不变量。

由此，欧拉示性数可作进一步推广。对于任意一个拓扑空间X，当求和存在时，这一整数称为拓扑空间X欧拉示性数。